安装必须的库:
# Install required packages.
import os
import torch
os.environ['TORCH'] = torch.__version__
print(torch.__version__)
!pip install -q torch-scatter -f https://data.pyg.org/whl/torch-${TORCH}.html
!pip install -q torch-sparse -f https://data.pyg.org/whl/torch-${TORCH}.html
!pip install -q git+https://github.com/pyg-team/pytorch_geometric.git
!pip install -q captum
# Helper function for visualization.
%matplotlib inline
import matplotlib.pyplot as plt复制
1.13.1+cu116
Installing build dependencies ... done
Getting requirements to build wheel ... done
Preparing metadata (pyproject.toml) ... done复制
用解释GNN模型的预测
在本教程中,我们演示了怎样将特点归属方式应用于图。具体来说,我们企图找到对每位实例预测最重要的边。
我们使用的诱变性数据集。这个数据集由4337个分子图组成,任务是预测分子的诱变性。
加载数据集
我们加载数据集并使用10%的数据作为测试分割。
from torch_geometric.loader import DataLoader
from torch_geometric.datasets import TUDataset
path = '.'
dataset = TUDataset(path, name='Mutagenicity').shuffle()
test_dataset = dataset[:len(dataset) // 10]
train_dataset = dataset[len(dataset) // 10:]
test_loader = DataLoader(test_dataset, batch_size=128)
train_loader = DataLoader(train_dataset, batch_size=128)复制
Downloading https://www.chrsmrrs.com/graphkerneldatasets/Mutagenicity.zip
Extracting ./Mutagenicity/Mutagenicity.zip
Processing...
Done!
复制
数据的可视化
我们定义了一些用于可视化分子的效用函数,并随机抽取一个分子。
import networkx as nx
import numpy as np
from torch_geometric.utils import to_networkx
def draw_molecule(g, edge_mask=None, draw_edge_labels=False):
g = g.copy().to_undirected()
node_labels = {}
for u, data in g.nodes(data=True):
node_labels[u] = data['name']
pos = nx.planar_layout(g)
pos = nx.spring_layout(g, pos=pos)
if edge_mask is None:
edge_color = 'black'
widths = None
else:
edge_color = [edge_mask[(u, v)] for u, v in g.edges()]
widths = [x * 10 for x in edge_color]
nx.draw(g, pos=pos, labels=node_labels, width=widths,
edge_color=edge_color, edge_cmap=plt.cm.Blues,
node_color='azure')
if draw_edge_labels and edge_mask is not None:
edge_labels = {k: ('%.2f' % v) for k, v in edge_mask.items()}
nx.draw_networkx_edge_labels(g, pos, edge_labels=edge_labels,
font_color='red')
plt.show()
def to_molecule(data):
ATOM_MAP = ['C', 'O', 'Cl', 'H', 'N', 'F',
'Br', 'S', 'P', 'I', 'Na', 'K', 'Li', 'Ca']
g = to_networkx(data, node_attrs=['x'])
for u, data in g.nodes(data=True):
data['name'] = ATOM_MAP[data['x'].index(1.0)]
del data['x']
return g复制
取样的可视化
我们从中抽出一个单分子并将其可视化
import random
data = random.choice([t for t in train_dataset])
mol = to_molecule(data)
plt.figure(figsize=(10, 5))
draw_molecule(mol)复制
训练模型
在下一节中,我们训练一个具有5个频域层的GNN模型。我们使用,它支持作为一个参数。的许多频域层都支持这个参数。
定义模型
import torch
from torch.nn import Linear
import torch.nn.functional as F
from torch_geometric.nn import GraphConv, global_add_pool
class Net(torch.nn.Module):
def __init__(self, dim):
super(Net, self).__init__()
num_features = dataset.num_features
self.dim = dim
self.conv1 = GraphConv(num_features, dim)
self.conv2 = GraphConv(dim, dim)
self.conv3 = GraphConv(dim, dim)
self.conv4 = GraphConv(dim, dim)
self.conv5 = GraphConv(dim, dim)
self.lin1 = Linear(dim, dim)
self.lin2 = Linear(dim, dataset.num_classes)
def forward(self, x, edge_index, batch, edge_weight=None):
x = self.conv1(x, edge_index, edge_weight).relu()
x = self.conv2(x, edge_index, edge_weight).relu()
x = self.conv3(x, edge_index, edge_weight).relu()
x = self.conv4(x, edge_index, edge_weight).relu()
x = self.conv5(x, edge_index, edge_weight).relu()
x = global_add_pool(x, batch)
x = self.lin1(x).relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.lin2(x)
return F.log_softmax(x, dim=-1)复制
定义训练和测试函数
def train(epoch):
model.train()
if epoch == 51:
for param_group in optimizer.param_groups:
param_group['lr'] = 0.5 * param_group['lr']
loss_all = 0
for data in train_loader:
data = data.to(device)
optimizer.zero_grad()
output = model(data.x, data.edge_index, data.batch)
loss = F.nll_loss(output, data.y)
loss.backward()
loss_all += loss.item() * data.num_graphs
optimizer.step()
return loss_all / len(train_dataset)
def test(loader):
model.eval()
correct = 0
for data in loader:
data = data.to(device)
output = model(data.x, data.edge_index, data.batch)
pred = output.max(dim=1)[1]
correct += pred.eq(data.y).sum().item()
return correct / len(loader.dataset)复制
对模型进行100次的训练
最后的确切率应当在80%左右
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(dim=32).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(1, 101):
loss = train(epoch)
train_acc = test(train_loader)
test_acc = test(test_loader)
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}, '
f'Train Acc: {train_acc:.4f}, Test Acc: {test_acc:.4f}')复制
Epoch: 090, Loss: 0.2992, Train Acc: 0.8824, Test Acc: 0.7968
Epoch: 091, Loss: 0.3000, Train Acc: 0.8855, Test Acc: 0.8060
Epoch: 092, Loss: 0.3129, Train Acc: 0.8832, Test Acc: 0.8037
Epoch: 093, Loss: 0.3056, Train Acc: 0.8791, Test Acc: 0.8129
Epoch: 094, Loss: 0.2947, Train Acc: 0.8835, Test Acc: 0.8014
Epoch: 095, Loss: 0.2949, Train Acc: 0.8758, Test Acc: 0.8129
Epoch: 096, Loss: 0.2946, Train Acc: 0.8791, Test Acc: 0.8060
Epoch: 097, Loss: 0.2989, Train Acc: 0.8768, Test Acc: 0.8083
Epoch: 098, Loss: 0.2946, Train Acc: 0.8822, Test Acc: 0.7968
Epoch: 099, Loss: 0.2908, Train Acc: 0.8835, Test Acc: 0.8060
Epoch: 100, Loss: 0.2910, Train Acc: 0.8840, Test Acc: 0.8037复制
解释预测结果
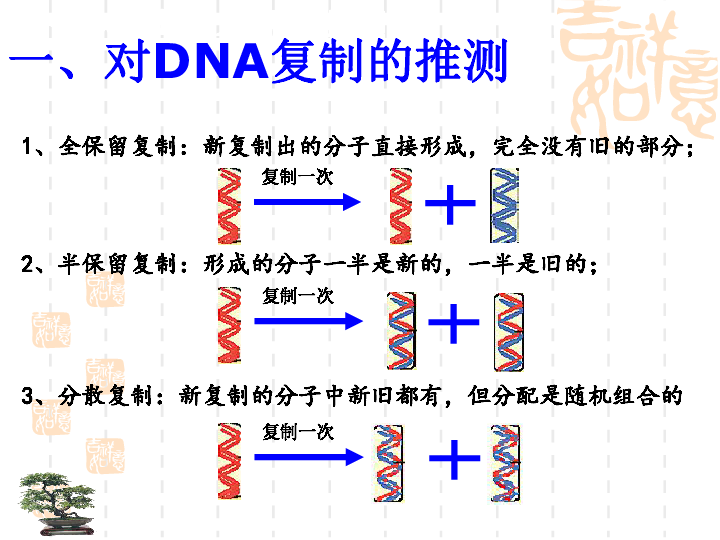
如今我们看一下两种流行的归因方式。首先,我们估算输出相对于边沿权重的梯度wei。边沿权重最初对所有的边沿都是一。对于明显性技巧,我们使用梯度的绝对值作为每位边沿的归属值。
其中x是输入,F(x)是GNN模型对输入x的输出。
对于综合梯度法,我们在当前输入和基线输入之间进行插补,其中所有边沿的权重为零,并累积每条边沿的梯度值。
其中xα与原始输入图相同,但所有边的权重被设置为α。综合梯度的完整叙述比较复杂,但因为我们的初始边权重等于1,基线为0,所以可以简化为上述叙述。你可以在这儿阅读更多关于这个方式的信息。其实,这不能直接估算,而是用一个离散的总和来近似。
我们使用库来估算归因值。我们定义了函数,假定我们一次只解释一个图形,它还会估算出批量参数。
from captum.attr import Saliency, IntegratedGradients
def model_forward(edge_mask, data):
batch = torch.zeros(data.x.shape[0], dtype=int).to(device)
out = model(data.x, data.edge_index, batch, edge_mask)
return out
def explain(method, data, target=0):
input_mask = torch.ones(data.edge_index.shape[1]).requires_grad_(True).to(device)
if method == 'ig':
ig = IntegratedGradients(model_forward)
mask = ig.attribute(input_mask, target=target,
additional_forward_args=(data,),
internal_batch_size=data.edge_index.shape[1])
elif method == 'saliency':
saliency = Saliency(model_forward)
mask = saliency.attribute(input_mask, target=target,
additional_forward_args=(data,))
else:
raise Exception('Unknown explanation method')
edge_mask = np.abs(mask.cpu().detach().numpy())
if edge_mask.max() > 0: # avoid division by zero
edge_mask = edge_mask / edge_mask.max()
return edge_mask复制
最后我们从测试数据集中随机抽取一个样本,运行解释方式。为了更简单的可视化,我们使图形无定向,并合并每位边沿在两个方向上的解释。
众所周知,在许多情况下,NO2的子结构使分子具有诱变性,你可以通过模型的解释来验证这一点。
在这个数据集中,诱变分子的标签为0,我们只从这种分子中采样su模型简化,但你可以改变代码su模型简化,也可以看见其他类别的解释。
在这个可视化中,边沿的颜色和长度代表了重要性。你也可以通过向函数传递来查看数值。
正如你所看见的,综合梯度常常能创造出更确切的解释。
import random
from collections import defaultdict
def aggregate_edge_directions(edge_mask, data):
edge_mask_dict = defaultdict(float)
for val, u, v in list(zip(edge_mask, *data.edge_index)):
u, v = u.item(), v.item()
if u > v:
u, v = v, u
edge_mask_dict[(u, v)] += val
return edge_mask_dict
data = random.choice([t for t in test_dataset if not t.y.item()])
mol = to_molecule(data)
for title, method in [('Integrated Gradients', 'ig'), ('Saliency', 'saliency')]:
edge_mask = explain(method, data, target=0)
edge_mask_dict = aggregate_edge_directions(edge_mask, data)
plt.figure(figsize=(10, 5))
plt.title(title)
draw_molecule(mol, edge_mask_dict)复制











请登录后查看回复内容